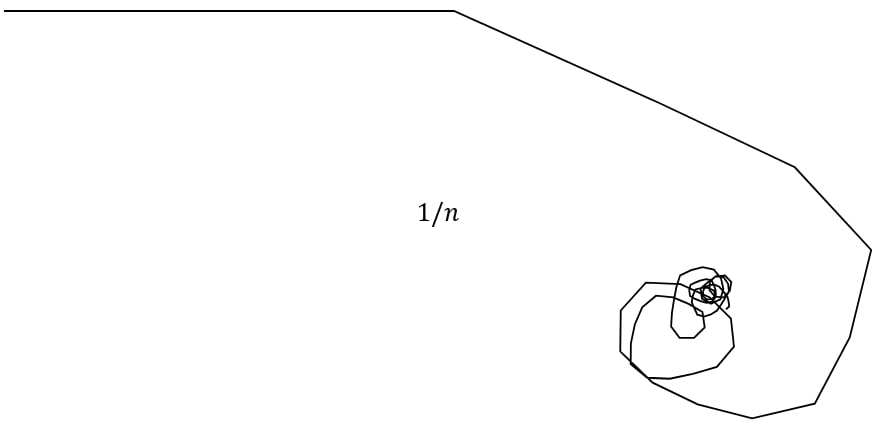
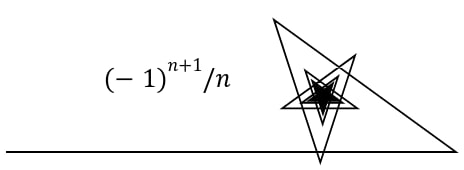
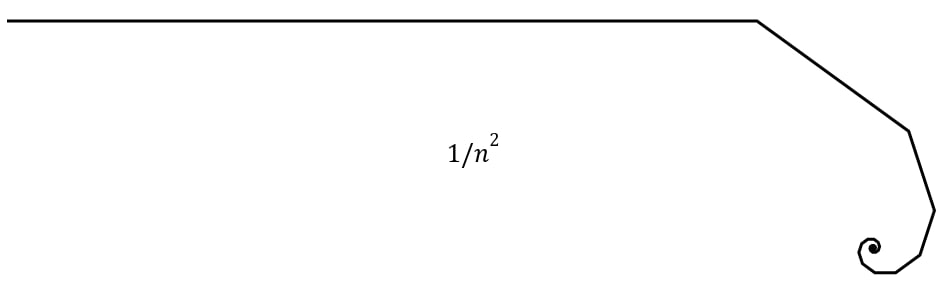Придумал забавную математическую задачку.
Я уже давал ссылку (↑) на видео про фрактальную размерность. Если говорить очень упрощённо, длина кривой зависит от того, какой длины линейку мы к ней прикладываем. Например, если измерять береговую линию какого-нибудь фьорда короткими измерительными шестами, она оказывается длиннее, чем если брать длинный шест. А если бы мы могли выпрямить кривую в прямую линию, она оказалась бы бесконечной длины. Но изгибы линии (которые происходят не только на крупном, а на всех масштабах) позволяют эту линию бесконечной длины нарисовать на плоскости. При этом такая фигура заполняет не всю плоскость, а только её часть. Поэтому ей можно сопоставить размерность между 1 и 2: это уже не совсем линия, но ещё не плоскость. Обычно такую размерность считают для фракталов (откуда её название), но вообще говоря, её можно посчитать для любого множества точек.
Так вот, задачка. Известно, что существуют сходящиеся и расходящиеся ряды.
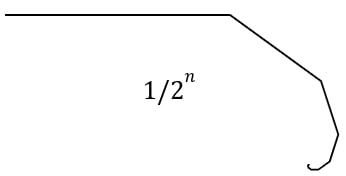
Например, сумма геометрической прогрессии ∑1/(2^n): 1 + 1/2 + 1/4 + 1/8 + … стремится к 2. Мы сложили бесконечное количество чисел, а получили конечный результат. Потому что прибавляемые числа всё меньше и меньше.
Сумма обратных квадратов ∑1/n²: 1 + 1/4 + 1/9 + 1/16 + … стремится к π²/6 (да, откуда-то из обычных квадратов чисел возникает число пи; по-моему, очень красиво!)
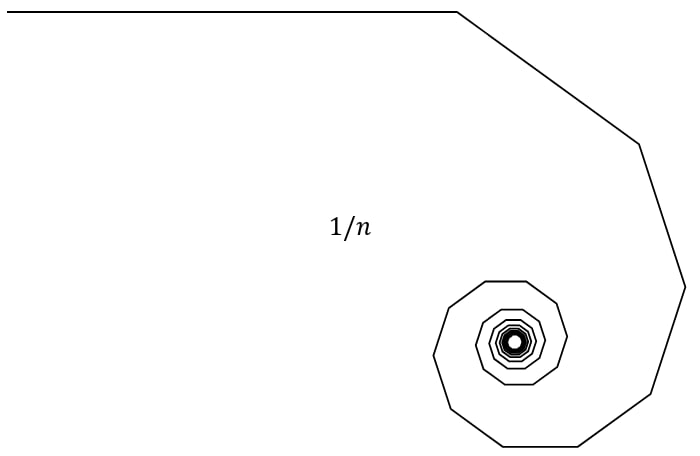
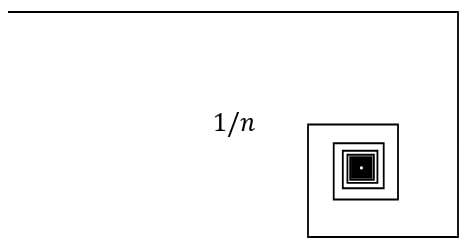
А вот сумма обратных чисел ∑1/n: 1 + 1/2 + 1/3 + 1/4 + 1/5 + … не сходится никуда. Члены последовательности уменьшаются слишком медленно, поэтому сумма оказывается бесконечной. Этот ряд называется гармоническим, что для меня загадочно, поскольку он как раз ломает всю гармонию.
Если мы нарисуем ломаную из отрезков длин 1/(2^n), то эту ломаную можно выпрямить в отрезок длины 2. Ломаную из отрезков длины 1/n² тоже можно выпрямить в отрезок длины π²/6. А вот ломаную из отрезков, составляющих гармонический ряд, можно выпрямить только в луч бесконечной длины. Но!
Мы ведь можем не выпрямлять ломаную! Вместо этого мы можем, например, каждое звено цепи поворачивать на какой-нибудь угол относительно предыдущей. И тогда у нас получится кривулина, заметающая какую-то часть плоскости. Её сложно было бы назвать «береговой линией», уж слишком странная страна должна для этого быть. Но определённо это кривая, у которой можно измерить фрактальную размерность.
Я не знаю, можно ли такую размерность вывести аналитически (я не придумал, как), но не должно быть большой проблемой провести численный эксперимент.
Сразу возникает куча вопросов:
— укладывается ли вообще закон масштабирования длины ломаной в зависимости от размера измерительной сетки в логику размерности Минковского?
— если укладывается, какая размерность у ломаной гармонического ряда? А у других известных рядов?
— зависит ли она от угла поворота звеньев ломаной?
— а вообще как правильно рисовать такую ломаную, чтобы она была несамопересекающейся?
— а как следовало бы трактовать отрицательные длины звеньев?
А если ставить более общий вопрос: можно ли корректно определить фрактальную размерность ряда? Как она себя ведёт при различных операциях над рядами?
upd: увы, увы. В комментах разобрались, что размерность будет единицей: одну особую точку можно покрыть одним шариком, а остаток ломаной одномерен.
Файл: fractal_one_over_n.html
fractal_one_over_n.html